Diese Seite funktioniert nur mit Javascript.
Faktornachfrage3.5.1.3 Angebotsfunktion einer BrancheMarkt- und Preistheorie
ie kurzfristige Angebotsfunktion einer Industrie beschreibt das aggregierte Angebot der einzelnen Unternehmen. Sie ist somit die aggregierte Grenzkostenkurve der Unternehmen und unter den üblichen Annahmen sehr einfach zu bestimmen. Wenn man nämlich von vollkommener Information ausgeht, verfügen alle Unternehmen über das gleiche Know How, d.h. die gleiche Technologie, und somit die gleichen Kostenfunktionen. Hat man also festgestellt, dass ein Unternehmen bei einem gegeben Preis die Menge $x$ anbietet, dann bieten 1000 Unternehmen die Menge $1000 \cdot x$ an. Lässt man zu, dass sich die Unternehmen in ihren Kostenfunktionen unterscheiden, gewinnt man ihre aggregierte Angebotsfunktion vollkommen analog zur aggregierten Nachfragefunktion in der Haushaltstheorie durch horizontale grafische Addition.
Auf lange Sicht muss jedoch bedacht werden, dass es zu Marktein- und Marktaustritten der Unternehmen kommen kann.
Aufgrund der Konkurrenzannahme bauen die Unternehmen keine Marktzutrittsbarrieren auf, da ein Unternehmen mehr oder weniger bei der "atomistischen" Konkurrenz nicht ins Gewicht fällt. Zudem würde jedes einzelne Unternehmen die Kosten der Errichtung solcher Barrieren scheuen, da es die Erträge nicht internalisieren könnte ("Trittbrettfahrer-Verhalten"). Bei anderen Marktformen wie dem Monopol oder dem engen Oligopol müsste man die Möglichkeit dieses strategischen Verhaltens, Wettbewerbern den Marktzutritt möglichst schwer zu machen, wenn nicht gar unmöglich zu machen, selbstverständlich beachten.
Ob und in welchem Ausmaß das langfristige Angebot über die Veränderung der Produktion in den Betrieben oder die Veränderung der Zahl der Betriebe auf Preisänderungen reagiert, hängt vor allem von der Technologie und somit vom Verlauf der langfristigen Kostenfunktionen ab. Betrachtet sei zunächst der Fall einer ertragsgesetzlichen Produktionstechnologie. In diesem Fall hat die Durchschnittskostenfunktion u-förmigen Verlauf (s. Abb. 1) und wird in ihrem Minimum (Betriebsoptimum) durch die Grenzkostenkurve geschnitten.
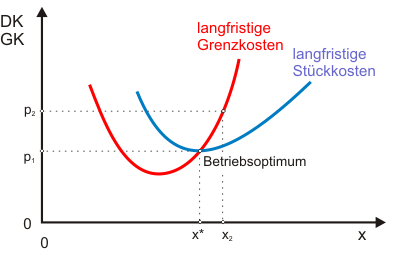
Bei einem Produktpreis in Höhe von $p_1$ wären weder Marktein- noch -austritte zu beobachten. Die Unternehmen befänden sich in einer Nullprofitsituation und die Konsumenten erhielten das Produkt zum auf Dauer günstigsten Preis.
Nun sei angenommen, der Preis steige auf $p_2$. Kurzfristig würde jedes Unternehmen im Markt die Produktion nach Maßgabe der kurzfristigen Grenzkostenkurve ausdehnen (Preis-Grenzkosten-Regel). Die kurzfristige Grenzkostenkurve ist in Abbildung 1 nicht eingezeichnet. Aus den Überlegungen zum Angebot einer einzelnen Unternehmung ist aber bekannt, dass sie im Betriebsoptimum steiler als die eingezeichnete langfristige Grenzkostenkurve verliefe. Zunächst wäre also eine relativ schwache Ausdehnung der Produktion zu beobachten.
In den Unternehmen würden nun Gewinne erzielt, und wenn die Preisänderung als dauerhaft eingeschätzt würde, würden Investitionen erfolgen, um das Einsatzverhältnis der Produktionsfaktoren wieder kostenminimal zu gestalten. Die Anpassung würde sich damit an der langfristigen Grenzkostenkurve gestalten, die Produktion auf x2 steigen.
Zahlenbeispiele zur Illustration
Zwei Zahlenbeispiele zur langfristigen Kosten- und Angebotsfunktion
Diese Situation ist aber nicht stabil. Die langfristigen Gewinnerwartungen führen zu Markteintritten. Es werden so lange Wettbewerber in den Markt eintreten, bis durch das gestiegene Angebot der Preis wieder auf das Ausgangsniveau gefallen ist, da bei jedem dauerhaft über dem Betriebsoptimum liegenden Preis auch auf Dauer Gewinne erzielt werden könnten. Auf lange Sicht wird bei der durch die u-förmige Durchschnittskostenfunktion eindeutig determinierten optimalen Betriebsgröße das Angebot über die Zahl der Unternehmen im Markt gesteuert.
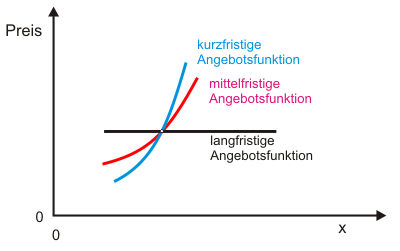
Wenngleich die Schlussfolgerungen hier auf einer recht unsicheren Basis stehen, weil Ergebnisse eines komparativ statischen Modells dynamisch interpretiert werden, darf man vermuten, dass Profite i.e.S. hier nur in den Übergangsphasen anfallen. Die Unternehmen, die am schnellsten auf Preisänderungen reagieren, können zwischenzeitlich Gewinne realisieren (oder bei fallenden Preisen Verluste vermeiden). Wenn an der Annahme vollkommener Information festgehalten wird, ist es aber letztlich zufallsbedingt, welche Unternehmen hier in den Markt eintreten können bzw. ausscheiden müssen.
Es gibt allerdings einen gewichtigen Grund, der gegen eine langfristig waagerecht verlaufende Angebotsfunktion spricht. Auf der Industrieebene führt die vermehrte Nachfrage nach Faktorleistungen, die bei steigender Produktion einsetzt, zu steigenden Preisen auf den Faktormärkten. Daher kann an der Annahme gegebener Preise auf allen Märkten nicht festgehalten werden. Selbst wenn alle Produktionsfaktoren, die man in der Betriebswirtschaftslehre als Elementarfaktoren bezeichnen würde, unendlich elastisch angeboten würden, kann man davon ausgehen, dass der dispositive Faktor knapp wird: die Bereitschaft und die Fähigkeit, unternehmerisch tätig zu sein (Managementfähigkeiten) und das damit verbundene Risiko zu tragen (Unternehmertum). Demzufolge würden nur bei steigenden Risikoprämien Wettbewerber in den Markt eintreten wollen. Dann aber würde das Betriebsoptimum nicht mehr bei allen Unternehmen die gleiche Höhe (im Beispiel p1) haben, und daher die langfristige Angebotsfunktion ansteigen. Steigende Gütermengen wären dann auch langfristig nur bei steigenden Preisen verfügbar.
Nun stellt natürlich der bisher angenommene Fall einer u-förmigen langfristigen Durchschnittskostenfunktion nur eine Möglichkeit dar. Es ist allerdings relativ unwahrscheinlich, dass die Funktion im gesamten Bereich ansteigenden Verlauf zeigt. Das würde ja bedeuten, die optimale Betriebsgröße läge bei Null. Ein langfristig fallenden Verlauf der Durchschnittskostenfunktion wäre mit der Marktform vollkommener Konkurrenz nicht vereinbar (Gesetz der Massenproduktion, natürliches Monopol). Bei langfristig konstanten Skalenerträgen - die Niveauproduktionsfunktion verliefe linear - wären die Durchschnittskosten konstant und die optimale Betriebsgröße unbestimmt. In diesem Fall wäre bereits für die einzelne Unternehmung die langfristige Angebotsfunktion vollkommen elastisch.
Zusammenfassendes Diagramm
Jedes andere Ergebnis hätte aber auch verwundern müssen, da Konkurrenz ja gerade so definiert wurde, dass sich die Unternehmen Gewinne gegenseitig "wegkonkurrieren". Kurz- und mittelfristig wird aber auch auf Konkurrenzmärkten das Gesetz des Angebots gelten. Und selbst langfristig wird man ein mit steigenden Preisen wachsendes Angebot beobachten, da auf Industrieniveau nicht alle Produktionsfaktoren in beliebigen Mengen zu konstanten Preisen verfügbar sein werden.